大家好，我是小?，一个漂泊江湖多年的 985 非科班程序员，曾混迹于国企、互联网大厂和创业公司的后台开发攻城狮。

1. 引言

当我那天拿着手机，正在和朋友们的微信群里畅聊着八卦新闻和即将到来的周末计划时，忽然一条带着喜意的消息扑面而来，消息正中间赫然写着八个大字：恭喜发财，大吉大利。

图片

抢红包！！相信大部分人对此都不陌生，自 2015 年春节以来，微信就新增了各类型抢红包功能，吸引了数以亿万级的用户参与体验，今天，我们就来聊一聊这个奇妙有趣的红包系统。

2. 概要设计

2.1 系统特点

图片

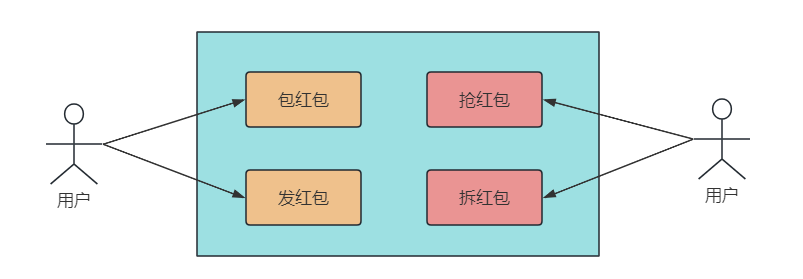
抢红包系统从功能拆分，可以分为包红包、发红包、抢红包和拆红包 4 个功能。

对于系统特性来说，抢红包系统和秒杀系统类似。

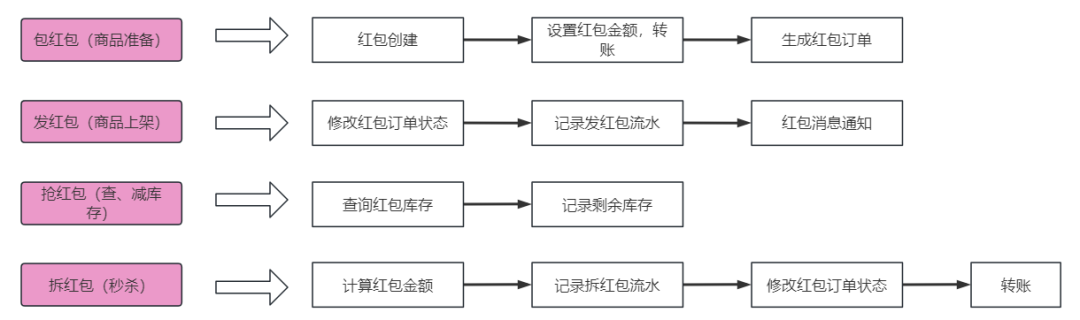图片

每次发红包都是一次商品秒杀流程，包括商品准备，商品上架，查库存、减库存，以及秒杀开始，最终的用户转账就是红包到账的过程。

2.2 难点

相比秒杀活动，微信发红包系统的用户量更大，设计更加复杂，需要重视的点更多，主要包括以下几点。

1、高并发

海量并发请求，秒杀只有一次活动，但红包可能同一时刻有几十万个秒杀活动。

比如 2017 鸡年除夕，微信红包抢红包用户数高达 3.42 亿，收发峰值 76 万/秒，发红包 37.77 亿 个。

2、安全性要求

红包业务涉及资金交易，所以一定不能出现超卖、少卖的情况。

• 超卖：发了 10 块钱，结果抢到了 11 块钱，多的钱只能系统补上，如此为爱发电应用估计早就下架了；
• 少卖：发了 10 块钱，只抢了 9 块，多的钱得原封不动地退还用户，否则第二天就接到法院传单了。

3、严格事务

参与用户越多，并发 DB 请求越大，数据越容易出现事务问题，所以系统得做好事务一致性。

这也是一般秒杀活动的难点所在，而且抢红包系统涉及金钱交易，所以事务级别要求更高，不能出现脏数据。

3. 概要设计

3.1 功能说明

抢红包功能允许用户在群聊中发送任意个数和金额的红包，群成员可以抢到随机金额的红包，但要保证每个用户的红包金额不小于 0.01 元。

图片

抢红包的详细交互流程如下：

1. 用户接收到抢红包通知，点击通知打开群聊页面；
2. 用户点击抢红包，后台服务验证用户资格，确保用户尚未领取过此红包；
3. 若用户资格验证通过，后台服务分配红包金额并存储领取记录；
4. 用户在微信群中看到领取金额，红包状态更新为“已领取”；
5. 异步调用支付接口，将红包金额更新到钱包里。

3.2 数据库设计

红包表 redpack 的字段如下：

• id： 主键，红包ID
• userId： 发红包的用户ID
• totalAmount： 总金额
• surplusAmount： 剩余金额
• total： 红包总数
• surplusTotal： 剩余红包总数

该表用来记录用户发了多少红包，以及需要维护的剩余金额。

红包记录表 redpack_record 如下：

• id： 主键，记录ID
• redpackId： 红包ID，外键
• userId： 用户ID
• amount： 抢到的金额

记录表用来存放用户具体抢到的红包信息，也是红包表的副表。

3.3 发红包

1. 用户设置红包的总金额和个数后，在红包表中增加一条数据，开始发红包；
2. 为了保证实时性和抢红包的效率，在 Redis 中增加一条记录，存储红包 ID 和总人数 n；
3. 抢红包消息推送给所有群成员。

3.4 抢红包

从 2015 年起，微信红包的抢红包和拆红包就分离了，用户点击抢红包后需要进行两次操作。

这也是为什么明明有时候抢到了红包，点开后却发现该红包已经被领取完了。

图片

抢红包的交互步骤如下：

1. 抢红包：抢操作在 Redis 缓存层完成，通过原子递减的操作来更新红包个数，个数递减为 0 后就说明抢光了。
2. 拆红包：拆红包时，首先会实时计算金额，一般是通过二倍均值法实现（即 0.01 到剩余平均值的 2 倍之间）。
3. 红包记录：用户获取红包金额后，通过数据库的事务操作累加已经领取的个数和金额，并更新红包表和记录表。
4. 转账：为了提升效率，最终的转账为异步操作，这也是为什么在春节期间，红包领取后不能立即在余额中看到的原因。

上述流程，在一般的秒杀活动中随处可见，但是，红包系统真的有这么简单吗？

当用户量过大时，高并发下的事务一致性怎么保证，数据分流如何处理，红包的数额分配又是怎么做的，接下来我们一一探讨。

4. 详细设计

由于是秒杀类设计，以及 money 分发，所以我们重点关注抢红包时的高并发解决方案和红包分配算法。

4.1 高并发解决方案

首先，抢红包系统的用户量很大，如果几千万甚至亿万用户同时在线发抢红包，请求直接打到数据库，必然会导致后端服务过载甚至崩溃。

而在这种业务量下，简单地对数据库进行扩容不仅会让成本消耗剧增，另一方面由于存在磁盘的性能瓶颈，所以大概率解决不了问题。

所以，我们将解决方案集中在 减轻系统压力、提升响应速度 上，接下来会从缓存、加锁、异步分治等方案来探讨可行性。

1、缓存

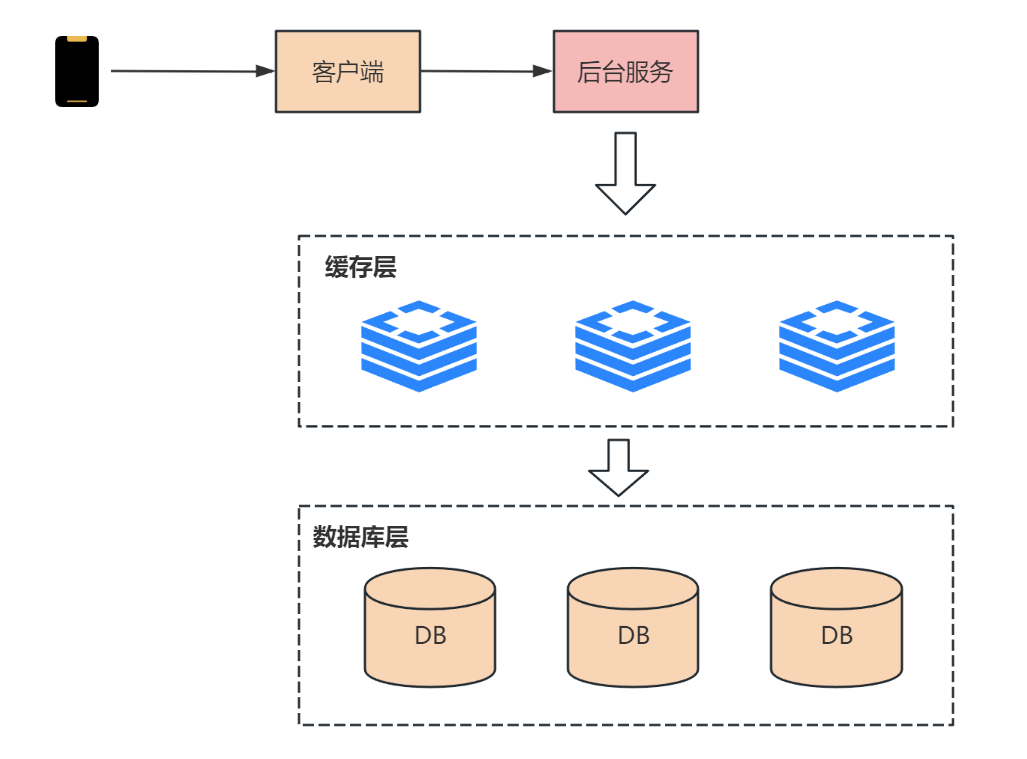
和大多数秒杀系统设计相似，由于抢红包时并发很高，如果直接操作 DB 里的数据表，可能触发 DB 锁的逻辑，导致响应不及时。

图片

所以，我们可以在 DB 落盘之前加一层缓存，先限制住流量，再处理红包订单的数据更新。

这样做的优点是用缓存操作替代了磁盘操作，提升了并发性能，这在一般的小型秒杀活动中非常有效！

但是，随着微信使用发&抢红包的用户量增多，系统压力增大，各种连锁反应产生后，数据一致性的问题逐渐暴露出来：

• 假设库存减少的内存操作成功，但是 DB 持久化失败了，会出现红包少发的问题；
• 如果库存操作失败，DB 持久化成功，又可能会出现红包超发的问题。

而且在几十万的并发下，直接对业务加锁也是不现实的，即便是乐观锁。

2、加锁

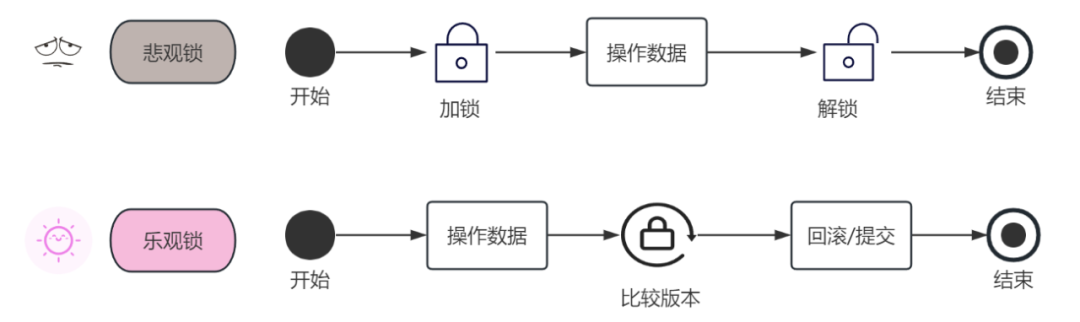
在关系型 DB 里，有两种并发控制方法：分为乐观锁（又叫乐观并发控制，Optimistic Concurrency Control，缩写 “OCC”）和悲观锁（又叫悲观并发，Pessimistic Concurrency Control，缩写“PCC”）。

图片

悲观锁在操作数据时比较悲观，认为别的事务可能会同时修改数据，所以每次操作数据时会先把数据锁住，直到操作完成。

乐观锁正好相反，这种策略主打一个“信任”的思想，认为事务之间的数据竞争很小，所以在操作数据时不会加锁，直到所有操作都完成到提交时才去检查是否有事务更新（通常是通过版本号来判断），如果没有则提交，否则进行回滚。

在高并发场景下，由于数据操作的请求很多，所以乐观锁的吞吐量更大一些。但是从业务来看，可能会带来一些额外的问题：

1. 抢红包时大量用户涌入，但只有一个可以成功，其它的都会失败并给用户报错，导致用户体验极差；
2. 抢红包时，如果第一时间有很多用户涌入，都失败回滚了。过一段时间并发减小后，反而让手慢的用户抢到了红包；
3. 大量无效的更新请求和事务回滚，可能给 DB 造成额外的压力，拖慢处理性能。

总的来说，乐观锁适用于数据竞争小，冲突较少的业务场景，而悲观锁也不适用于高并发场景的数据更新。

因此对于抢红包系统来说，加锁是非常不适合的。

3、异步分治

综上所述，抢红包时不仅要解决高并发问题、还得保障并发的顺序性，所以我们考虑从队列的角度来设计。

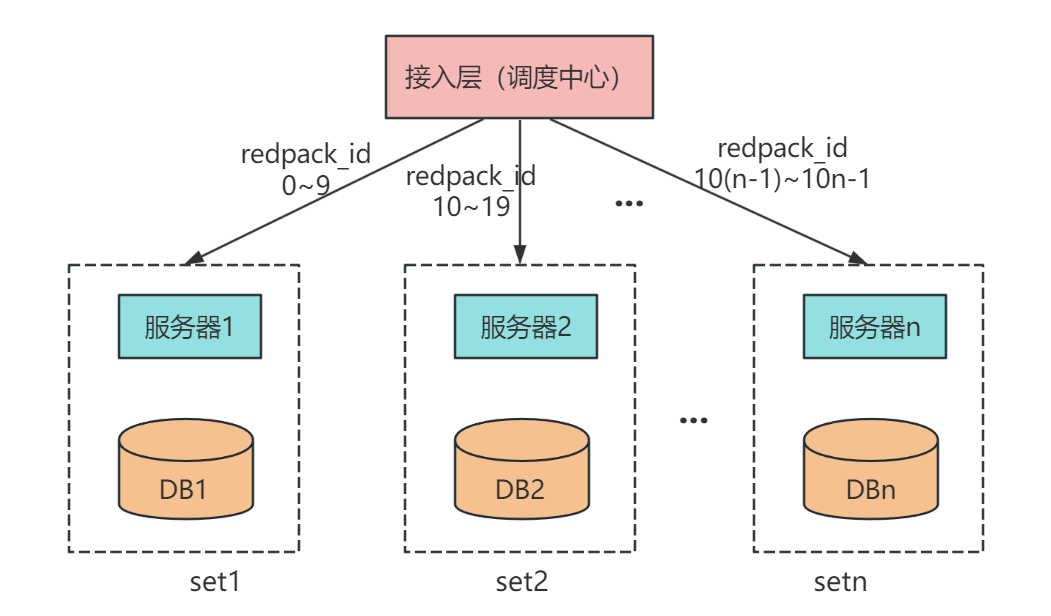
我们知道，每次包红包、发红包、抢红包时，也有先后依赖关系，因此我们可以将红包 ID 作为一个唯一 Key，将发一次红包看作一个单独的 set，各个 set 相互独立处理。

图片

这样，我们就把海量的抢红包系统分成一个个的小型秒杀系统，在调度处理中，通过对红包 ID 哈希取模，将一个个请求打到多台服务器上解耦处理。

然后，为了保证每个用户抢红包的先后顺序，我们把一个红包相关的操作串行起来，放到一个队列里面，依次消费。

从上述 set 分流我们可以看出，一台服务器可能会同时处理多个红包的操作，所以，为了保证消费者处理 DB 不被高并发打崩，我们还需要在消费队列时用缓存来限制并发消费数量。

抢红包业务消费时由于不存储数据，只是用缓存来控制并发。所以我们可以选用大数据量下性能更好的 Memcached。

除此之外，在数据存储上，我们可以用红包 ID 进行哈希分表，用时间维度对 DB 进行冷热分离，以此来提升单 set 的处理性能。

综上所述，抢红包系统在解决高并发问题上采用了 set 分治、串行化队列、双维度分库分表 等方案，使得单组 DB 的并发性能得到了有效提升，在应对数亿级用户请求时取得了良好的效果。

4.2 红包分配算法

抢红包后，我们需要进行拆红包，接下来我们讨论一下红包系统的红包分配算法。

红包金额分配时，由于是随机分配，所以有两种实现方案：实时拆分和预先生成。

1、实时拆分

实时拆分，指的是在抢红包时实时计算每个红包的金额，以实现红包的拆分过程。

这个对系统性能和拆分算法要求较高，例如拆分过程要一直保证后续待拆分红包的金额不能为空，不容易做到拆分的红包金额服从正态分布规律。

2、预先生成

预先生成，指的是在红包开抢之前已经完成了红包的金额拆分，抢红包时只是依次取出拆分好的红包金额。

这种方式对拆分算法要求较低，可以拆分出随机性很好的红包金额，但通常需要结合队列使用。

3、二倍均值法

综合上述优缺点考虑，以及微信群聊中的人数不多（目前最高 500 人），所以我们采用实时拆分的方式，用二倍均值法来生成随机红包，只满足随机即可，不需要正态分布。

故可能出现很大的红包差额，但这更刺激不是吗??

使用二倍均值法生成的随机数，每次随机金额会在 0.01 ~ 剩余平均值*2 之间。

假设当前红包剩余金额为 10 元，剩余个数为 5，10/5 = 2，则当前用户可以抢到的红包金额为：0.01 ~ 4 元之间。

4、算法优化

用二倍均值法生成的随机红包虽然接近平均值，但是在实际场景下：微信红包金额的随机性和领取的顺序有关系，尤其是金额不高的情况下。

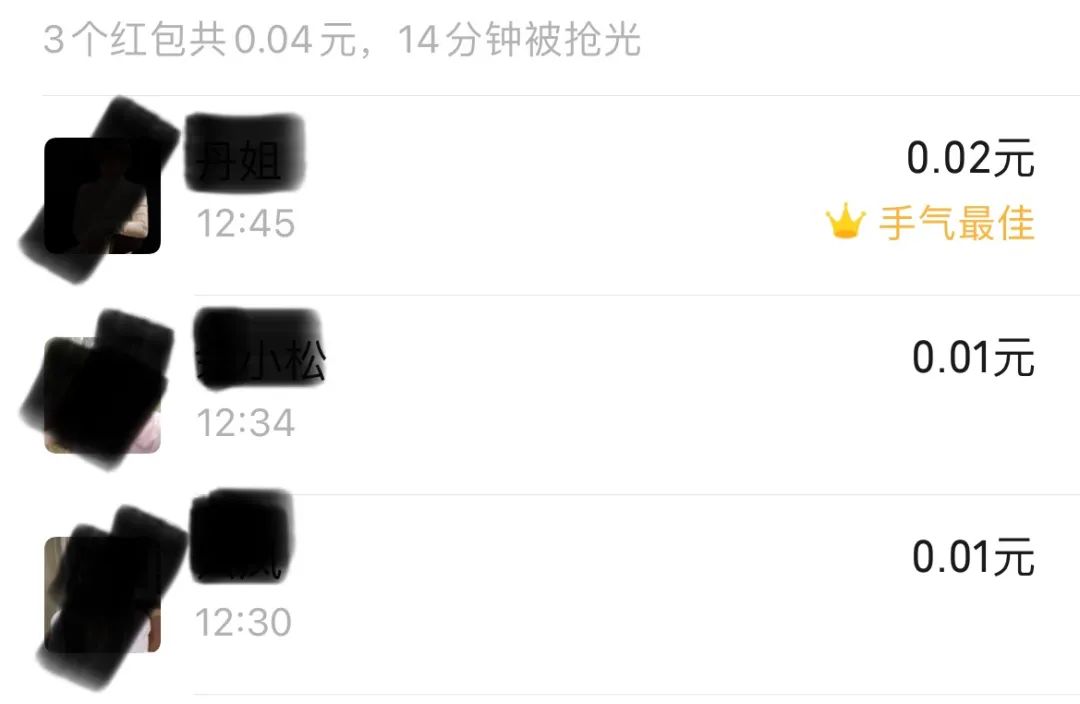
于是，小?耗费 “巨资” 在微信群发了多个红包，得出了这样一个结论：如果发出的 红包总额 = 红包数*0.01 + 0.01，比如：发了 4 个红包，总额为 0.05，则最后一个人领取的红包金额一定是 0.02。

图片

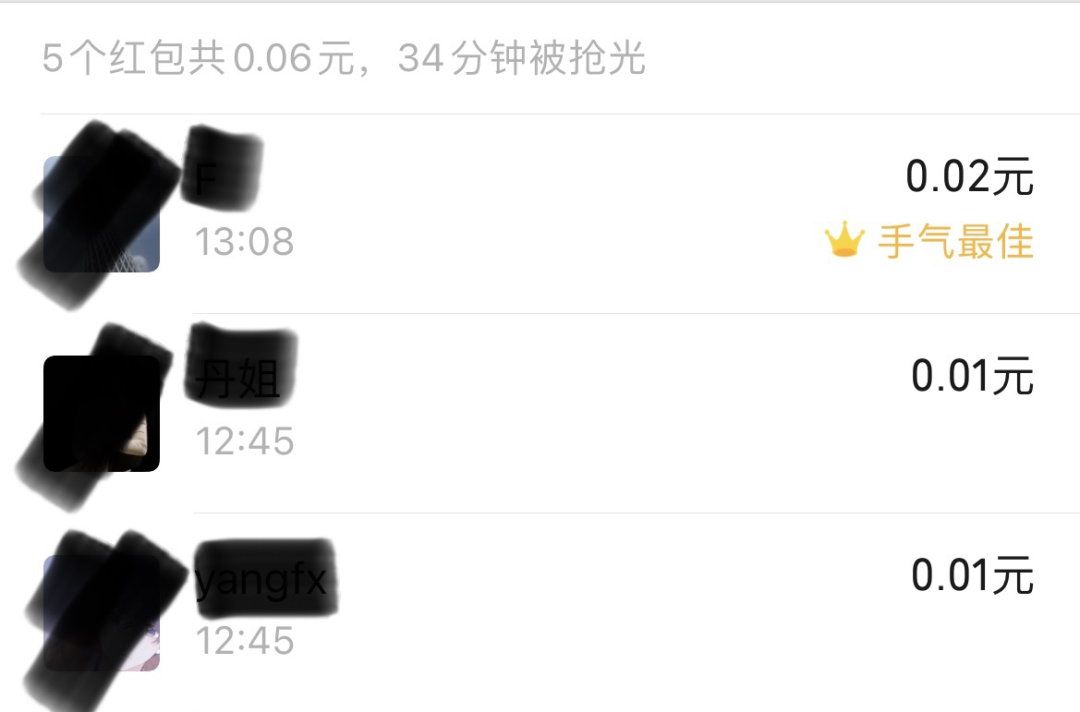
无一例外：

图片

所以，红包金额算法大概率不是随机分配，而是在派发红包之前已经做了处理。比如在红包金额生成前，先生成一个不存在的红包，这个红包的总额为 0.01 * 红包总数。

而在红包金额分配的时候，会对每个红包的随机值基础上加上 0.01，以此来保证每个红包的最小值不为 0。

所以，假设用户发了总额为 0.04 的个数为 3 的红包时，需要先提取 3*0.01 到 "第四个" 不存在的红包里面，于是第一个人抢到的红包随机值是 0 ~ (0.04-3*0.01)/3。

由于担心红包超额，所以除数的商是向下取二位小数，0 ~ (0.04-3*0.01)/3 ==> (0 ~ 0) = 0，再加上之前提取的保底值 0.01，于是前两个抢到的红包金额都是 0.01。最后一个红包的金额为红包余额，即 0.02。

算法逻辑用 Go 语言实现如下：

import (
   "fmt"
   "math"
   "math/rand"
   "strconv"
)

type RedPack struct {
    SurplusAmount float64 // 剩余金额
     SurplusTotal int // 红包剩余个数
}

// 取两位小数
func remainTwoDecimal(num float64) float64 {
    numStr := strconv.FormatFloat(num, 'f', 2, 64)
    num, _ = strconv.ParseFloat(numStr, 64)
    return num
}

// 获取随机金额的红包
func getRandomRedPack(rp *RedPack) float64 {
    if rp.SurplusTotal <= 0 {
        // 该红包已经被抢完了
        return 0
    }

    if rp.SurplusTotal == 1 {
        return remainTwoDecimal(rp.SurplusAmount + 0.01)
    }

       // 向下取整
    avgAmount := math.Floor(100*(rp.SurplusAmount/float64(rp.SurplusTotal))) / float64(100)
    avgAmount = remainTwoDecimal(avgAmount)

       // 生成随机数种子
    rand.NewSource(time.Now().UnixNano())

    var max float64
    if avgAmount > 0 {
        max = 2*avgAmount - 0.01
    } else {
        max = 0
    }
    money := remainTwoDecimal(rand.Float64()*(max) + 0.01)

    rp.SurplusTotal -= 1
    rp.SurplusAmount = remainTwoDecimal(rp.SurplusAmount + 0.01 - money)

    return money
}

// 实现主函数
func main() {
    rp := &RedPack{
        SurplusAmount: 0.06,
        SurplusTotal:  5,
    }
    rp.SurplusAmount -= 0.01 * float64(rp.SurplusTotal)
    total := rp.SurplusTotal
    for i := 0; i < total; i++ {
        fmt.Println(getRandomRedPack(rp))
    }
}