合作机构:阿里云 / 腾讯云 / 亚马逊云 / DreamHost / NameSilo / INWX / GODADDY / 百度统计
资讯热度排行榜
- 157751政务云服务应突出“服务”含
- 36622政务云解决方案
- 36283电子政务应用系统发展的几个
- 10334B 站标签系统落地实践
- 10055必会的七个数据可视化库
- 9566通过数据目录集中数据治理
- 9547行业观察 | 增强分析是下
- 94682024年大数据行业预测(
- 9229四种SVM主要核函数及相关
- 910102024年大数据展望:数据
推荐阅读
- 12-061数据科学家95%的时间都在使用的
- 12-132数据驱动业务方法
- 12-213什么是数据湖?
- 12-2642024年的14个大数据预测
- 12-295如何做销售数据分析?
- 01-0862024年大数据行业预测(一)
- 01-097如何利用数据库流服务进行实时分析
- 01-258应避免的八个数据战略错误
- 01-289第三方抢票软件不比官方快:铁路
- 01-11102024年,在云平台,开启全球外
数据科学家95%的时间都在使用的11个基本分布
继上次盘点《数据科学家95%的时间都在使用的11个基本图表》之后,今天将为大家带来数据科学家95%的时间都在使用的11个基本分布。掌握这些分布,有助于我们更深入地理解数据的本质,并在数据分析和决策过程中做出更准确的推断和预测。

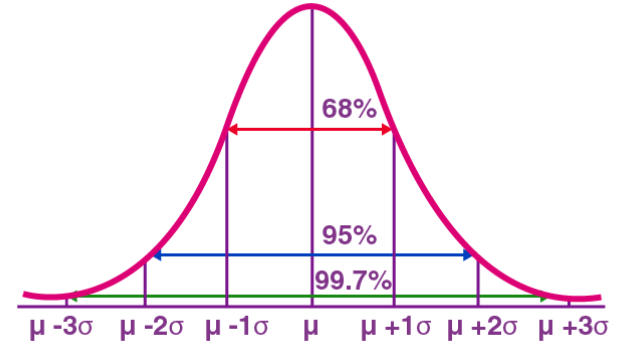
1. 正态分布
正态分布(Normal Distribution),也被称为高斯分布(Gaussian Distribution),是一种连续型概率分布。它具有一个对称的钟形曲线,以均值(μ)为中心,标准差(σ)为宽度。正态分布在统计学、概率论、工程学等多个领域具有重要的应用价值。
正态分布的概率密度函数为:

其中,μ是均值,σ是标准差。概率密度函数表示在给定值x附近,单位区间内正态分布的随机变量取值的概率密度。
正态分布在实际中的应用:例如人的身高和体重分布近似于正态分布;考试成绩通常呈正态分布,高分和低分的人数较少,中间分数的人数较多。
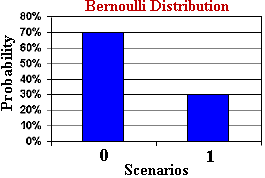
2. 伯努利分布
伯努利分布(Bernoulli Distribution)是一种离散型概率分布,用于描述只有两种可能结果的单次随机试验。伯努利试验可以是正面或反面,成功或失败,是或否等。例如,抛硬币、检测产品是否合格、某人是否购买某种产品等。
伯努利分布的概率质量函数为:
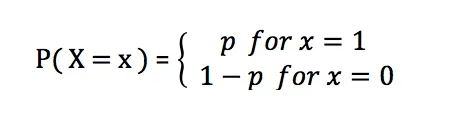
其中,p是成功的概率,取值范围在0和1之间。当p=0.5时,伯努利分布趋近于均匀分布。
伯努利分布在实际中的应用:例如二项分布就是伯努利分布的n次独立重复试验。
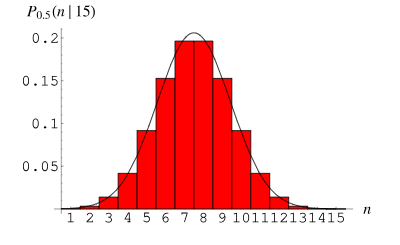
3. 二项分布
二项分布(Binomial Distribution)是一种离散型概率分布,用于描述在n次独立重复试验中成功次数的概率分布。每次试验只有两种可能的结果:成功(记为1)或失败(记为0)。成功的概率为p,失败的概率为1-p。
二项分布的概率质量函数为:
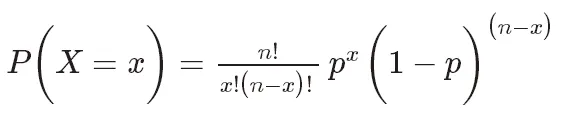
其中,P(X=k)表示成功次数为k的概率,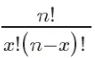 是组合数,表示从n次试验中选择k次成功的组合数。p是成功的概率,取值范围在0和1之间。n是试验次数。
是组合数,表示从n次试验中选择k次成功的组合数。p是成功的概率,取值范围在0和1之间。n是试验次数。
二项分布在实际中的应用:如在医学研究中,患者接受某种治疗的成功率;在工程中,产品在生产过程中的合格率等。
4. 泊松分布
泊松分布(Poisson Distribution)是一种离散型概率分布,用于描述在固定时间内,事件发生的次数的概率分布。泊松分布适用于那些事件相互独立,且平均发生速率恒定的情况。
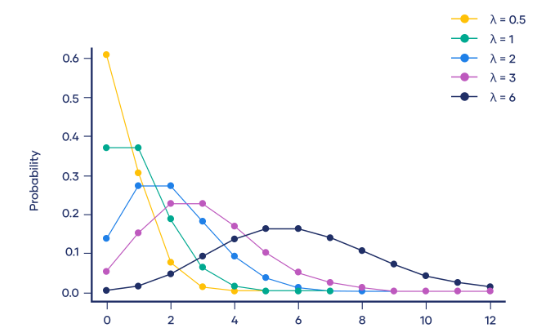
泊松分布的概率质量函数为:
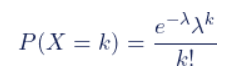
其中,P(X=k)表示在固定时间内事件发生k次的概率,λ表示事件的平均发生速率,即在单位时间内事件发生的平均次数。e是自然常数,约为2.718。k是事件发生的次数。
泊松分布在实际中的应用:例如在电话呼叫中心,每分钟打进的电话数量可以看作是泊松分布,平均每分钟打进的电话数量即为λ。
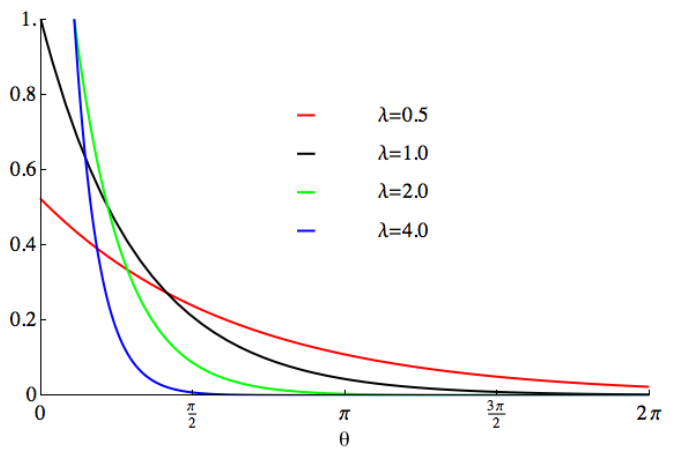
5. 指数分布
指数分布(Exponential Distribution)是一种连续型概率分布,用于描述在固定时间内,事件发生的概率。指数分布适用于那些事件相互独立,且平均发生速率恒定的情况。
指数分布的概率密度函数为:
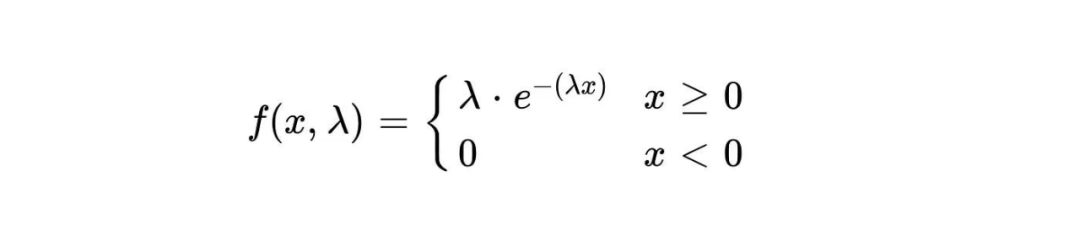
其中,f(x,λ)表示在给定时间x内事件发生的概率密度。λ表示事件的平均发生速率,即在单位时间内事件发生的平均次数。e是自然常数,约为2.718。
指数分布在实际中的应用:放射性衰变中,放射性原子核衰变的时间可以看作是指数分布,平均衰变时间即为λ。
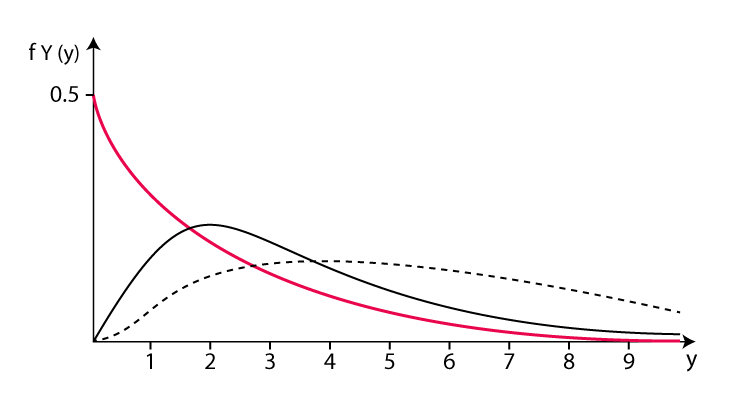
6. 伽玛分布
伽玛分布(Gamma Distribution)是一种连续型概率分布,用于描述在给定时间内,事件发生的概率。伽玛分布适用于那些事件相互独立,且平均发生速率恒定的情况。
伽玛分布的概率密度函数为:
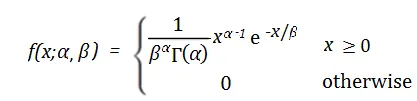
其中,f(x)表示在给定时间x内事件发生的概率密度。α和β分别表示形状参数和速率参数。α决定了伽玛分布的形状,取值范围为0到正无穷。β表示事件的平均发生速率,即在单位时间内事件发生的平均次数,取值范围为0到正无穷。e是自然常数,约为2.718。
伽玛分布在实际中的应用:例如放射性衰变:在放射性衰变中,放射性原子核衰变的时间可以看作是伽玛分布,平均衰变时间即为β/α。
7. 贝塔分布
贝塔分布(Beta distribution)是一种连续型概率分布,用于描述一组数值中成功次数的概率分布。它具有两个参数,分别表示成功概率的期望值(mean)和标准差(standard deviation)。
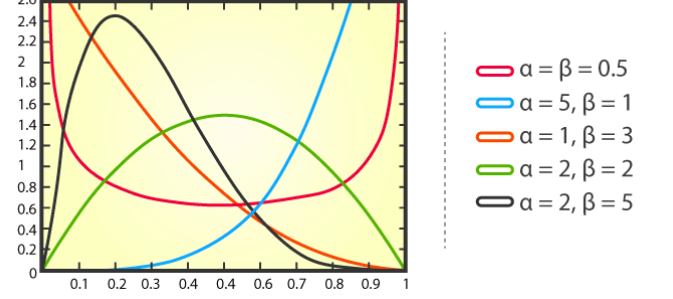
贝塔分布的概率密度函数如下:
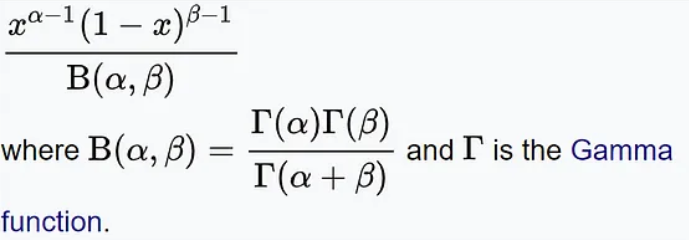
其中,x表示成功的次数,α和β分别表示分布的形状参数。
贝塔分布在许多实际问题中都有应用,例如,在基因编辑中,研究人员可能会使用贝塔分布来预测基因编辑技术成功编辑某个目标位点的概率。在金融领域,贝塔分布可以用于描述资产价格的波动性,或者用于计算投资组合的预期收益。
8. 均匀分布
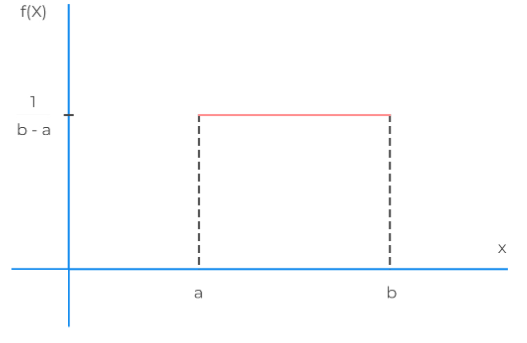
均匀分布是一种概率分布,用于描述一组数值在某个区间内均匀地分布。均匀分布有两种类型:离散均匀分布和连续均匀分布。
离散均匀分布:如果一个离散随机变量X具有以下概率分布:P(X=k) = k/(n+1),其中k为非负整数,n为区间内的整数,那么称X服从离散均匀分布。连续均匀分布:如果一个连续随机变量X的概率密度函数为f(x) = 1/(b-a)!
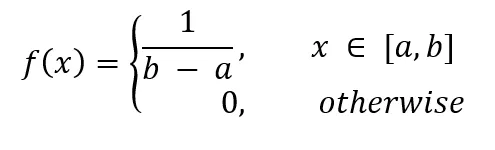
均匀分布的特点是,在给定的区间内,每个数值都有相同的机会出现。例如,抛一枚公正的硬币,正面和反面出现的概率都是1/2,这就是一种均匀分布。
9. 对数正态分布
对数正态分布(Log-normal distribution)是一种连续型概率分布,它的特点是随机变量的对数服从正态分布。换句话说,如果一个随机变量X的对数ln(X)服从正态分布,那么这个随机变量X就服从对数正态分布。
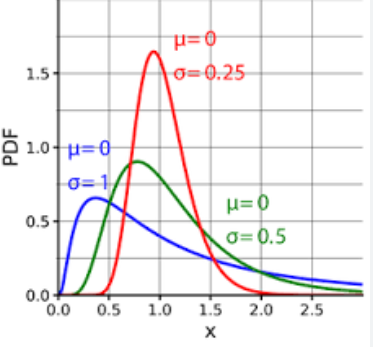
对数正态分布的概率密度函数为:
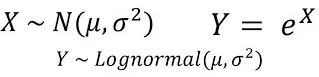
其中,μ是对数正态分布的均值,σ是对数正态分布的标准差。
对数正态分布在许多实际应用中都有重要意义,例如金融领域(股票价格、收益率等)、生物学(生长速率等)、经济学(消费支出等)等。
10. T分布
T分布,是一种连续型概率分布,主要用于小样本情况下描述均值的分布。t分布与正态分布(Normal distribution)类似,但它的尾部可以向左右延伸,取决于自由度(k)的大小。t分布广泛应用于统计推断,例如在假设检验中用于评估样本均值与总体均值之间的显著性差异。
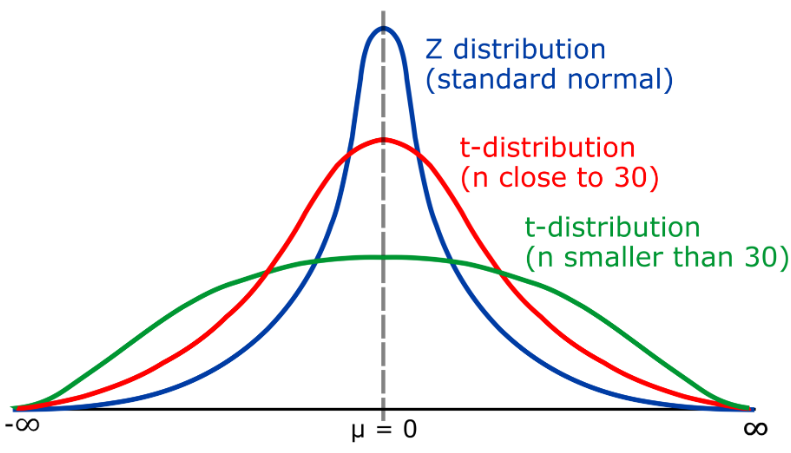
t分布的期望和方差如下:
E(t)=0
Var(t)=k/(k-1)
t分布的自由度(k)表示的是样本size(n)与总体标准差之间的关系。当 k > 30时,t分布接近正态分布;当k接近1时,t分布变为柯西分布(Cauchy distribution)。
在实际应用中,当样本量较大(n>30)时,可以使用正态分布来进行假设检验,此时可以使用z统计量构建置信区间。而当样本量较小(n<30)时,由于正态分布的假设不满足,需要使用t分布来进行检验。通过t分布,可以更准确地评估样本均值与总体均值之间的差异,从而做出合理的决策。
11. Weibull分布
Weibull分布(Weibull distribution)是一种连续型概率分布。
Weibull分布的概率密度函数为:
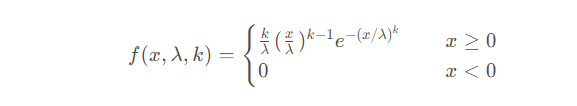
其中, x是随机变量,λ是比例参数(scale),k是形状参数(shape),当 k = 1时,韦伯分布是指数分布。而如果λ=1时,则称为最小化的韦伯分布。
-
TOP


